Digital advertising is subject to the law of diminishing returns: The more you spend, the less each dollar buys. Because of that, holdout tests are misleading when deciding how to allocate budget between advertising efforts.

The optimal allocation of budget between channels is one that has each channel operating at the same marginal return on ad spend (marginal ROAS). That’s a fancy way of saying that we want the cost of one more unit of KPI (click, lead, dollar of revenue, or whatever we’re optimizing for) to be equal across all channels. If it isn’t, then we’d be better off reducing spend in the more expensive channels in favor of the cheaper channels until they’re equalized. We can think of this as buying less KPI in our expensive channels, and more than making up for it by shifting those dollars to cheaper channels where they go further.

How can we measure marginal ROAS?

Many advertising gurus say that the gold standard for incrementality is the holdout test: divide the population in two, switch off ads to one part, and attribute the difference to the ads being tested. What that’s measuring is the overall effectiveness of your channel (what would happen if the channel were switched off vs on), rather than the rate at which additional dollars buy additional KPI.

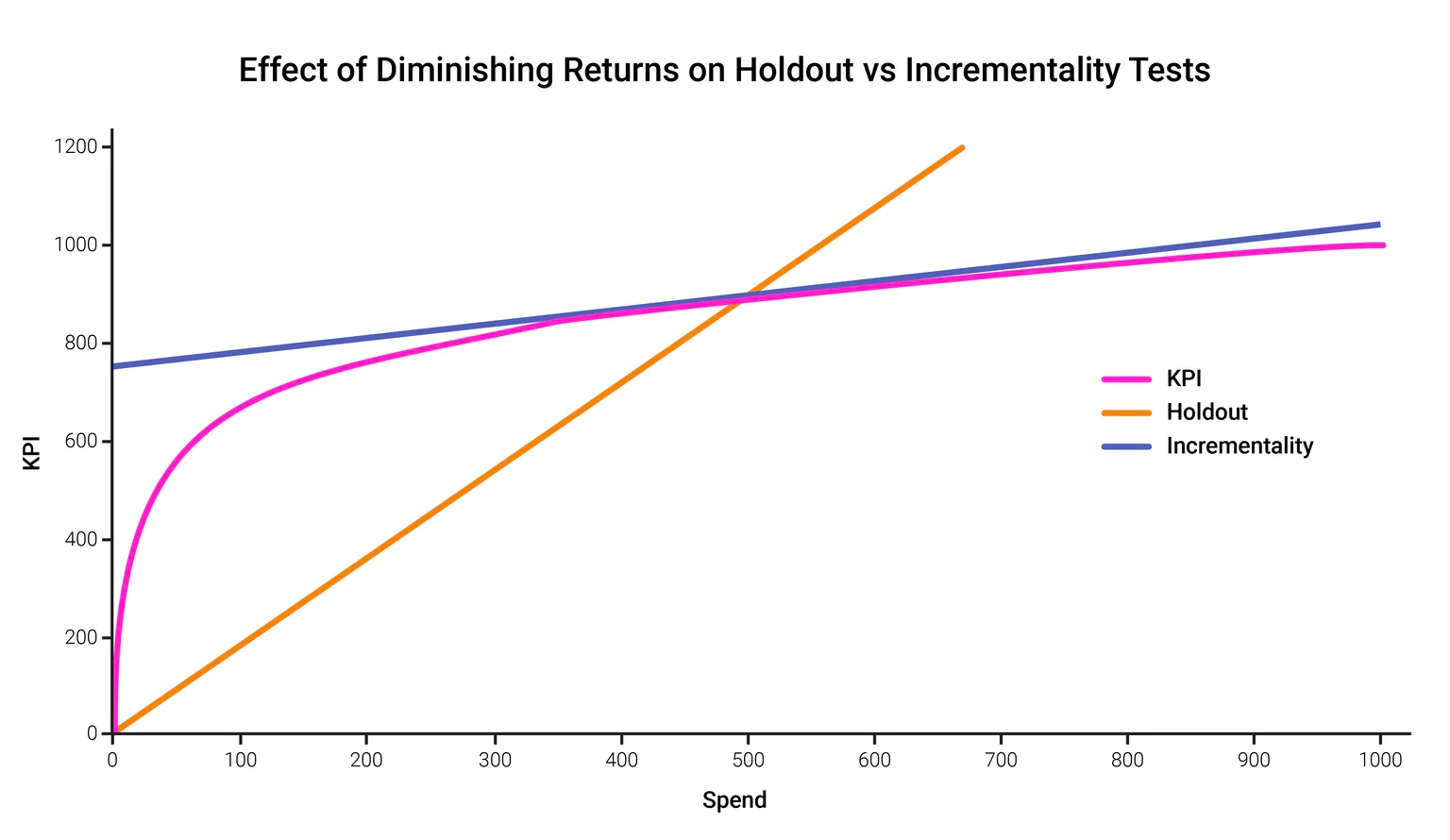
Let’s say the chart above shows channel spend on the x-axis, and some KPI we care about on the Y-axis. I’m keeping the numbers small, but we can assume both of these are in units of thousands. We want to evaluate the effectiveness of spending more money relative to a current spend level of 500. The black line shows the reality that we’re trying to estimate: how much KPI we would buy at different spend levels.

Under a holdout test, with perfect measurements (ignoring noise), we’d measure that:

• Holdout group: We get 0 KPI for 0 Spend
• Test group: we get 897 KPI for 500 Spend
• Our ROAS is 897 / 500 = 1.79. This is the average ROAS of spend between 0 & 500.

This correctly measures how much KPI we’re buying for our 500 of spend, but doesn’t tell us how much more KPI each additional dollar of spend will buy, so isn’t a measure of incrementality. The red line shows what we learn from a holdout test. While it’s correct at 0 and at 500, it very quickly diverges from reality as spend diverges from 500.

To measure incremental or marginal ROAS, i.e. the effect of small changes to spend relative to current spend, we conduct a different but similar test. We still divide our population into two groups, but instead of using a holdout, we raise spend on one group and lower it on the other.

Under an incrementality test, with perfect measurements (again ignoring noise), we’d measure that:

• Spend down: We get 881 KPI for 450 spend
• Spend up: We get 910 KPI for 550 spend
• Our marginal ROAS is (change in KPI) / (change in spend) = (910-881)/(550-450) = 0.29.

As you can see, the results are very different. The reason is that we’re advertising at a point on the curve that’s well into diminishing returns. While the average dollar is buying 1.79 KPI, our incremental dollar only buys 0.29 more KPI. The green line shows what we learn from an incrementality test. While this diverges from reality as we move away from 500 of spend, for spend levels near 500 it’s a good estimate of how our KPIs will change as spend goes up or down.

To illustrate how we might use incrementality testing to make decisions, let’s say we have a second channel with an average ROAS of 1.25 and a marginal ROAS of 0.75.

• Channel A: Average ROAS = 1.79, Marginal ROAS = 0.29
• Channel B: Average ROAS = 1.25, Marginal ROAS = 0.75

In this scenario, the effect of moving a unit of spend from channel A to channel B is:

• We buy 0.29 less KPI from A, and 0.75 more from B, a net gain of 0.46
• Our overall spend is unchanged
• The Marginal and Average ROAS of A increase slightly
• The Marginal and Average ROAS of B decrease slightly.

Moving spend from A to B will continue to be profitable until the marginal ROAS of the two channels are equal.

Had we been making the same decision on the basis of holdout tests, we’d be moving money in the opposite direction and losing 0.46 KPI for each unit of spend shifted.